艺考生数学考试都丢分的要点有哪些?
艺考生于数学考试之际,往往易在如下关键要点之处出现丢分情况:举例而言,部分同学在瞧见某道题目自认为能够解答之时,便会放松应有的警惕,采取跳步答题之方式,进而引发不必要的分数损失;需知数学符号皆有着极为严格的规定,诸如属于符号(∈)、正弦(sin)、余弦(cos)等等皆在此列。
一、基础知识部分
1.公式定理记忆不清:
数学中有大量的公式和定理,艺考生由于在数学学习上投入时间相对较少,可能对一些基本公式、定理的记忆不够准确。例如,三角函数的二倍角公式、等差数列和等比数列的通项公式及求和公式等,在考试时容易出现记错、混淆的情况,从而导致后续解题错误。
对于一些推导过程较为复杂的定理,如立体几何中的一些线面垂直、面面垂直的判定定理,艺考生可能没有深入理解其内涵,只是机械记忆,在应用时就无法准确判断条件是否满足,进而出现失分。

2.概念理解模糊:
数学概念是构建知识体系的基石,但艺考生可能对某些概念的理解存在偏差。比如函数的概念,包括定义域、值域、对应法则等方面,如果对这些概念理解不透彻,在做函数相关的题目时,就可能出现错误判断,像求函数定义域时忽略分母不能为零、偶次方根下被开方数非负等限制条件。
在概率统计部分,对一些基本概念如概率的定义、事件的独立性、随机变量的分布等理解不清,会导致在计算概率、期望、方差等问题时出现错误。
二、解题技巧与方法部分
1.缺乏解题思路:
面对一些综合性较强的题目,艺考生往往不知道从何处入手解题。例如,在解析几何题中,当遇到直线与圆锥曲线相交的问题时,需要联立方程,再利用韦达定理等进行后续计算,但艺考生可能由于缺乏这方面的解题思路,不知道要先联立方程,从而无法继续解题,导致丢分。
在数列题中,对于一些需要通过构造新数列来求解通项公式的题目,艺考生可能想不到构造的方法,只能眼睁睁看着题目却无法动笔,白白失分。
2.运算能力不足:
数学考试中运算量较大,艺考生可能在运算过程中出现各种错误。比如在进行分式运算时,通分、约分不当;在解一元二次方程时,求根公式运用错误或者在计算过程中出现符号错误等。
对于一些较为复杂的数值计算,如在立体几何中计算空间向量的夹角、模长等,艺考生可能由于心算、笔算能力不强,借助计算器又可能不熟练(高考部分地区允许使用计算器),从而导致运算结果错误,进而失分。

三、考试心态与习惯部分
1.紧张焦虑导致失误:
艺考生面对数学考试时,由于自身数学基础相对薄弱,往往会比较紧张焦虑。这种不良心态可能会导致在考试中出现一些低级错误,比如看错题目要求,把“求最大值”看成“求最小值”;或者在填写答题卡时,将答案填错位置等。
紧张情绪还可能影响解题速度,使得艺考生在规定时间内无法完成所有题目,即使后面的题目会做,也只能遗憾失分。
2.粗心大意的习惯:
艺考生在数学考试中经常会出现粗心大意的情况。例如,在计算过程中忽略了题目中的一些关键条件,如“不包括端点值”等;或者在书写答案时,忘记化简,写出的答案不规范,如根式没有化简、分式没有约分等,这些都会导致丢分。
四、复习疏漏部分
1.重点难点把握不准:
由于艺考生复习时间有限,可能无法准确把握数学学科的重点难点内容。比如在复习函数这一板块时,可能没有重点关注函数的单调性、奇偶性、最值等重要性质的深入理解和应用,而在考试中这些恰恰是经常考查的知识点,从而导致失分。
在复习导数部分时,可能没有深入理解导数的几何意义、导数在函数单调性、极值、最值等方面的应用,使得在考试中遇到相关题目时无法准确解答。
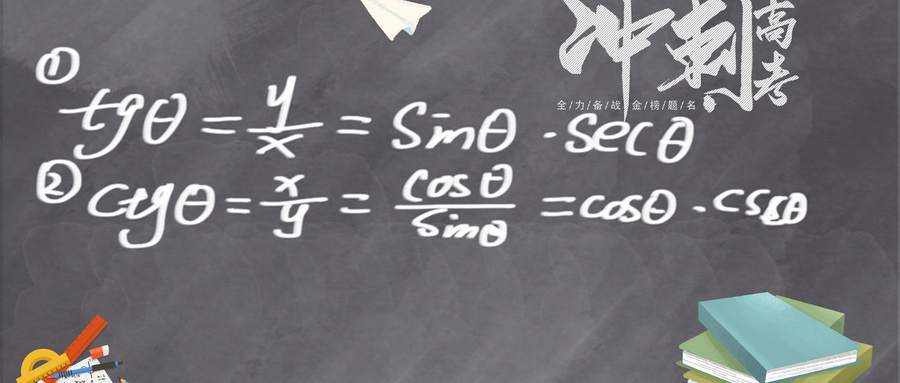
2.忽视错题分析:
艺考生在平时练习和模拟考试后,可能没有认真分析错题,找出自己的错误原因和薄弱环节。这样就无法有针对性地进行复习和改进,导致在同样的问题上反复出错,在正式考试中也会因此而丢分。
推荐课程
-

重庆三中英才小学奥数辅导班 教学点:21个 人气:1502
-

重庆三中英才高三数学辅导班 教学点:21个 人气:768
-

重庆三中英才高三全科冲刺班 教学点:21个 人气:727
-

重庆三中英才高三理科补习班 教学点:21个 人气:702
-

重庆三中英才高一全科辅导班 教学点:21个 人气:648
-

重庆三中英才高二全科补习班 教学点:21个 人气:622
咨询问答
- 同类机构
- 课程分类
- 班级列表
- 重庆三中英才高考冲刺班多少钱?附收费标准
- 重庆三中英才高三艺考文化课补习班可不可靠?
- 重庆三中英才高三冲刺补习班多少钱?性价比高吗?
- 重庆三中英才高考冲刺班全科辅导教师好吗?
- 重庆三中英才2025年高三艺考文化课冲刺辅导班收费详情
- 重庆三中英才高三艺考文化课辅导课程教得好吗?
- 重庆效果好的中小学课外辅导教学机构名单一览表
- 重庆三中英才高二一对一补课班要多少钱?怎么收费?
- 重庆三中英才高中课外补习班的费用贵不贵?
- 重庆三中英才高二课外一对一辅导课程要多少钱?
- 重庆三中英才高二课外辅导班的老师如何?好不好?
- 重庆三中英才2024年高考复读班的效果怎么样?
- 重庆三中英才暑假新高一辅导补习收费标准介绍
- 重庆三中英才高三复读课程效果怎么样?要多少费用?
- 重庆靠谱的高考复读补习机构十大排行榜
- 重庆三中英才小学奥数培训班什么时候开课?
- 重庆三中英才幼小衔接辅导课程什么时候开班?
- 重庆幼小衔接培训机构十大排名表
- 重庆三中英才幼小衔接班实力怎么样?教得好吗?
- 重庆三中英才幼小衔接辅导班实力怎么样?要多少钱?
- 重庆巴南区三中英才小学奥数培训好不好?
- 重庆九龙坡区三中英才小学奥数培训班
- 重庆沙坪坝三中英才小学奥数培训班
- 重庆三中英才渝北校区小学奥数辅导班
- 重庆三中英才江北区小学奥数学习班
- 重庆三中英才初升高培训课程有效果吗?值得去吗?
- 重庆三中英才初升高培训班效果好吗?
- 重庆三中英才高三冲刺班怎么样?效果好吗?
- 重庆三中英才高考冲刺培训班怎么样?靠谱吗?
- 重庆三中英才小学奥数培训班好不好?要多少学费?
- 重庆三中英才小学奥数辅导班有没有用?
- 重庆三中英才高三全托寒假辅导课程开班一览
- 重庆三中英才艺考文化课全日制补习课程要多少钱?
- 重庆艺考文化课小班辅导机构怎么选?选哪家?
- 重庆三中英才艺考文化课小班辅导有效果吗?好不好?
- 重庆三中英才艺考文化课全日制补习课程开班介绍
- 重庆三中英才高考一对一冲刺班收费标准是多少?
- 重庆三中英才一对一高中艺考文化课辅导班好不好?
- 重庆艺术生文化课培训机构十大排名
- 重庆三中英才高考冲刺培训课程效果好不好?
- 重庆沙坪坝三中英才奥数培训班性价比如何?
- 重庆奥数培训机构收费标准一览
- 重庆沙坪坝三中英才奥数培训班实力怎么样?
- 重庆三中英才奥数培训课程靠不靠谱?
- 重庆三中英才奥数培训课程好不好?
- 重庆三中英才小学奥数培训课程靠谱吗?
- 重庆三中英才少儿硬笔书法培训课程好不好?
- 重庆三中英才少儿硬笔书法培训班学习了哪些内容?
- 重庆三中英才准高三暑假集训课程适合哪些学生?
- 重庆三中英才高三全科暑假辅导课程开班啦
- 重庆三中英才高中英语暑假补习班学习了哪些内容?
- 重庆三中英才高中数学一对一暑假补习课程开班介绍
- 重庆三中英才小学奥数培训班要多少钱?
- 重庆三中英才少儿美术培训班效果怎么样?
- 重庆三中英才少儿口才表达课效果怎么样?靠谱吗?
- 重庆三中英才少儿口才培训班值不值得选?
- 重庆三中英才少儿口才培训班收费多少?学费贵吗?
- 重庆三中英才少儿口才表达课程开班介绍
- 重庆三中英才奥数培训课程开班啦
- 重庆三中英才高三艺考文化课集训班报名地址
- 重庆三中英才艺考文化课补习课程开班信息
- 重庆三中英才高考冲刺寒假补习班费用一览
- 重庆三中英才艺考文化课辅导班报名地址
- 重庆三中英才艺考文化课辅导班学习内容介绍
- 重庆九龙坡三中英才艺考文化课补习班开班信息
- 重庆三中英才高三艺考文化课补习班靠谱吗?
- 重庆三中英才高三艺考文化课补习班好不好
- 重庆三中英才高三艺考文化课补习班值得选吗?
- 重庆三中英才高三艺考文化课补习班学习内容有哪些?
- 重庆三中英才高三艺考文化课补习班教学实力如何?
- 重庆三中英才高三全科补习班报名方式
- 重庆三中英才高三全科培训班学习了哪些内容?
- 重庆三中英才高三全科一对一培训班培训内容介绍
- 重庆三中英才高三全科一对一培训班校区地址
- 重庆三中英才高三全科补习课程开班介绍
- 重庆三中英才艺考文化课培训班收费标准
- 重庆三中英才艺考文化课辅导班老师教的怎么样?
- 重庆三中英才艺考文化课辅导课程效果好不好?
- 重庆三中英才艺考文化课补习班报名地址在哪?
- 重庆三中英才艺考文化课补习班效果怎么样?
- 重庆三中英才高三集训班收费标准
- 重庆三中英才南开校区初中数学培训班
- 重庆三中英才小学数学辅导课程开班介绍
- 重庆三中英才语文(妙笔奥语)辅导课程开班介绍
- 重庆三中英才高中物理辅导班开班介绍
- 重庆三中英才高中英语暑假1对1辅导班开班介绍
- 重庆三中英才初中化学辅导班
- 重庆三中英才小学全科辅导班
- 重庆三中英才艺考生文化课辅导班学习了哪些内容?
- 重庆三中英才小学数学培训班
- 重庆三中英才高三集训复读班开课啦
- 重庆三中英才初中数学一对一辅导班
- 重庆三中英才新高一暑期课程班
关于我们 | 联系我们 | 咨询电话:4006-303-880
川ICP备07505283号
以上信息知识产权归“重庆三中英才中小学辅导学校”所有,并对内容的真实性和合法性负责,如有侵权或投诉,请联系我们处理。